Понятие нормы. Нормы векторов в конечномерном пространстве.

Если x и y – элементы линейного пространства X: x X, y X, то и x+y X, и ax X, где a R.

Определение. Линейное пространство- нормированное, если каждому его элементу x ставится в соответствие вещественное число, называемое нормой и обозначаемое ||x||, такое, что оно удовлетворяет следующим трем аксиомам:

1. ||x||³0, причем ||x||=0 только для x=0; (аксиома неотрицательности)

2. ||αx||=|α|·||x||, где a R; (аксиома однородности)

3. ||x+y||£||x||+||y||. (аксиома треугольника)

Норма – это обобщение модуля вещественного числа на элементы линейного пространства. Нормированным пространством является множество n-мерных векторов с вещественными координатами

x= . (n - число измерений)

Это пространство обозначается Rⁿ. Для него широко используются следующие три нормы:

1. ||x||_¥=max |x_i|, где 1£i£n; (норма-максимум)

2. ||x||₁= ; (норма-сумма)

3. ||x||₂= ²; (евклидова норма)

В конечномерном пространстве Rⁿ все нормы вектора эквивалентны(существуют такие константы m и M для произведения нормы, справедливо:

m||x||_β£||x||_α£M||x||_β,

где m и M – константы, не зависящие от элемента x.)

Так, например, поскольку

max(x_i)²£x²₁+x₂²+…+x_n²£n´max(x_i)², (максимум по i) то справедливо ||x||_¥£||x||₂£ 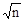||x||_¥ , т.е. здесь m=1, а M= .