Допустим, что на [a,b] функция f(x) меняется почти линейно. Тогда ее можно заменить стягивающей хордой y(x):
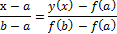
Точку пересечения хорды с осью абсцисс, где y(x1)=0 примем за первое приближение к корню исходного уравнения
аналогично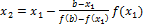 
Обобщая, получим расчетную формулу xn+1=xn- 
,
где X―неподвижный конец интервала. Для сходимости метода должны быть выполнены все условия теоремы о сходимости метода Ньютона, только условие f(X)•f"(X)>0 определяет выбор неподвижного конца; противоположный конец берется за начальное приближение: f(x0)•f "(x0)<0.
Геометрическая интерпретация метода хорд
