25.)
Из геометрической иллюстрации следует, что:
1. На каждом шаге есть погрешность (на рисунке это отрезок BD). Погрешность тем больше, чем больше шаг.
2. Ошибка может накапливаться.
Формула Эйлера 
имеет погрешность метода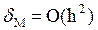 
Для практического выбора h с целью обеспечения заданной точности решения задачи e применяется следующий прием.
Выполняются 2 расчета: с n и 2n узлами. Если полученные значения функции в во всех узлах отличаются не более чем на e, задача считается решенной. Если нет, число узлов вновь удваивают и опять сравнивают полученные значения функций.
Таким образом, расчет продолжается до достижения условия
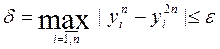
Порядок оценки погрешности метода Эйлера на одном шаге:
1)Записать разложение точного решения задачи Коши в точке 
по формуле Тейлора с остаточным членом в форме Лагранжа:
, 
.
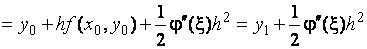2)Погрешность метода на одном шаге имеет порядок 
так как
3)После 
шагов погрешность вычисления значения 
в конечной точке отрезка возрастёт не более чем в раз. Погрешность метода Эйлера можно оценить неравенством
или представить в виде
,
где 
.
