1. Матрица симметрична относительно главной диагонали, то есть
.
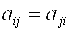2. Матрица является положительно определенной. Следовательно, при решении методом Гаусса можно воспользоваться схемой единственного деления.
3. Определитель матрицы будет отличен от нуля, если в качестве базиса выбраны линейно независимые функции 
; в этом случае система (7.18) имеет единственное решение.
В качестве базисных можно выбрать линейно независимые степенные функции
(7.23)
Следует учесть, чтоN << K. Тогда для этих функций расширенная матрица Грама примет вид
(7.24)
Если выбрать N = K, то на основании единственности интерполяционного полинома получим функцию 
, совпадающую с каноническим интерполяционным полиномом степени K. При этом аппроксимирующая кривая пройдет через все экспериментальные точки, и функция S будет равна нулю.
22.)
| Отыскание параметров эмпирических формул методом наименьших квадратов.
| 
| 
| 
|
При эмпирическом (экспериментальном) изучении функциональной зависимости одной величины У
от другой Х производят ряд измерений величины У при различных значениях величины Х.
Полученные результаты можно представить в виде таблицы, графика:
| X
| X1
| X2
| …
| Xn
| | Y
| Y1
| Y2
| …
| Yn
| |
