Решение систем обыкновенных дифференциальных уравнений.

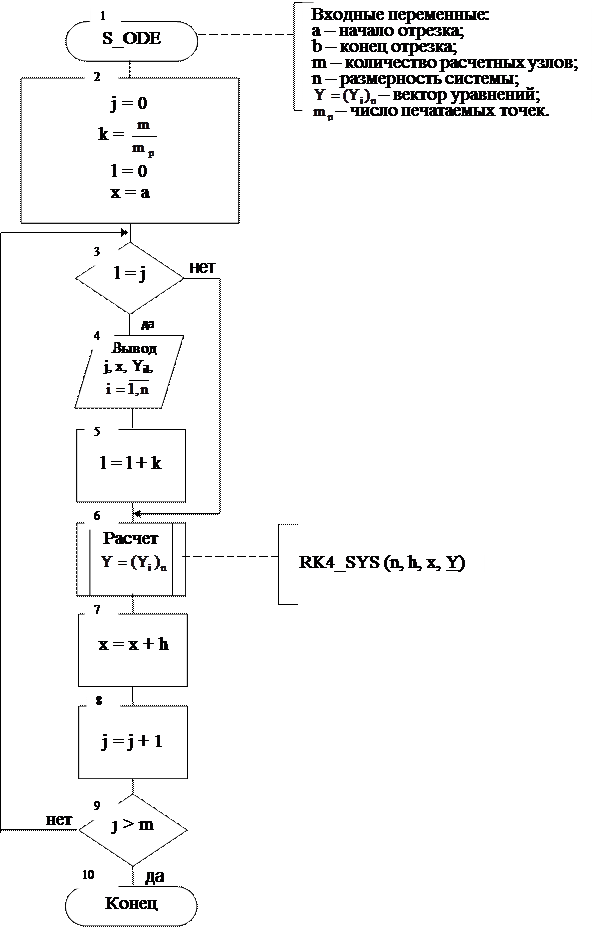
Системой дифференциальных уравнений называется система вида

где x - независимый аргумент, , где n – размерность системы.

y_i - зависимая функция, ,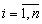

y_i|_x=x0 =y_i0 - начальные условия.

Функции y_i(x), при подстановке которой система уравнений обращается в тождество, называется решением системой дифференциальных уравнений.

Решение системы дифференциальных уравнений методом Эйлера:

y_ij+1=y_ij+hf_i(x_i,y_1j y_2j..y_nj)

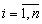
j - номер шага.

x_j+1=x_j+h

Модифицированный метод Эйлера.

k_i1=h*f_i(x_j,y_1j..y_nj)

k_i1=h*f_i(x_j+h,y_1j+k_i1..y_nj+k_i2)

y_ij+1=y_ij+(k_i1+k_i2)/2

x_j+1=x_j+h

Пусть задана система уравнений 1-го порядка:

y′ = f(x, y, z)

z′ = g(x, y, z)

с начальными условиями

y(x₀) = y₀ , z(x₀) = z₀ .

Приближенное решение системы определяется по формулам:

y_i+1 = y_i +∆y_i ,

z_i+1 = z_i + ∆z_i ,

где приращения ∆y_i и ∆z_i вычисляются в этом случае параллельно:

∆y_i = hf(x_i , y_i , z_i)

∆z_i = hg(x_i , y_i , z_i)

Формулы Эйлера-Коши для системы двух уравнений имеют следующий вид:

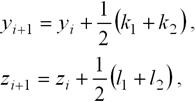
где

k₁ = hf(x_i , y_i , z_i),

l₁ = hg(x_i , y_i , z_i),

k₂ = hf(x_i+h, y_i+k₁ , z_i+l₁),

l₂ = hg(x_i+h, y_i+k₁ , z_i+l₁).