Однородным линейным дифференциальным уравнением второго порядка называется уравнение вида 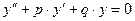 (1), где
(1), где  и
и 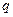 постоянны.
постоянны.
Частные решения уравнения (1) будем искать в виде  , где к – некоторое число. Дифференцируя эту функцию два раза и подставляя выражения для
, где к – некоторое число. Дифференцируя эту функцию два раза и подставляя выражения для  в уравнение (1), получим
в уравнение (1), получим  т.е.
т.е. 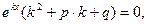 или
или  (2) (
(2) (  ).
).
Уравнение 2 называется характеристическим уравнением дифференциального уравнения.
При решении характеристического уравнения (2) возможны три случая.
Случай 1. Корни  и
и  уравнения (2) действительные и различные:
уравнения (2) действительные и различные:  . В этом случае частными решениями уравнения (1) являются функции
. В этом случае частными решениями уравнения (1) являются функции  и
и  . Следовательно, общее решение уравнения (1) имеет вид
. Следовательно, общее решение уравнения (1) имеет вид  .
.
Случай 2. Корни  и
и  уравнения (2) действительные и равные:
уравнения (2) действительные и равные:  . В этом случае частными решениями уравнения (1) являются функции
. В этом случае частными решениями уравнения (1) являются функции  и
и  . Следовательно, общее решение уравнения (1) имеет вид
. Следовательно, общее решение уравнения (1) имеет вид  .
.
Случай 3. Корни  и
и  уравнения (2) комплексные:
уравнения (2) комплексные:  ,
,  . В этом случае частными решениями уравнения (1) являются функции
. В этом случае частными решениями уравнения (1) являются функции  и
и  . Следовательно, общее решение уравнения (1) имеет вид
. Следовательно, общее решение уравнения (1) имеет вид 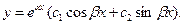
Пример.Решить уравнение .
.
Решение:составим характеристическое уравнение:  . Тогда
. Тогда  . Общее решение данного уравнения
. Общее решение данного уравнения  .
.