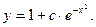Уравнение вида 
называется однородным, если 
и 
– однородные функции одного порядка (измерения). Функция 
называется однородной функцией первого порядка (измерения), если при умножении каждого ее аргумента на произвольный множитель 
вся функция умножиться на , т.е.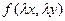 
= 
.
Однородное уравнение может быть приведено к виду 
. С помощью подстановки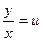 
( 
)однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к новой функции 
.
Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде 
.
Метод Бернулли
Решение уравнения ищется в виде произведения двух других функций, т.е. с помощью подстановки 
( 
).
Пример:проинтегрировать уравнение 
.
Полагаем . Тогда 
, т.е. 
. Сначала решаем уравнение 
=0: 
.
Теперь решаем уравнение 
т.е. 
. Итак, общее решение данного уравнения есть 
т.е. 
