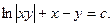Дифференциальное уравнение с разделенными переменными записывается в виде: 
(1).В этом уравнении одно слагаемое зависит только от x, а другое – от y. Проинтегрировав почленно это уравнение, получаем: 
– его общий интеграл.
Пример: найти общий интеграл уравнения: 
.
Решение: данное уравнение – дифференциальное уравнение с разделенными переменными. Поэтому 
или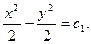 
Обозначим 
. Тогда 
– общий интеграл дифференциального уравнения.
Уравнение с разделяющимися переменными имеет вид 
(2).Уравнение (2)легко сводиться к уравнению (1) путем почленного деления его на 
. Получаем: 
– общий интеграл.
Пример:Решить уравнение
.
Решение: преобразуем левую часть уравнения: 
. Делим обе части уравнения на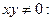 
Решением является выражение: 
т.е. 
