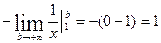Пусть функция  непрерывна на промежутке [a,+
непрерывна на промежутке [a,+  ). Если существует конечный предел
). Если существует конечный предел 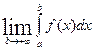 , то его называют несобственным интегралом первого рода и обозначают
, то его называют несобственным интегралом первого рода и обозначают  . Таким образом, по определению
. Таким образом, по определению  =
= 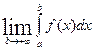
Аналогично определяется несобственный интеграл на промежутке (-  ,b];
,b];
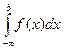 =
=  .
.
Несобственный интеграл с двумя бесконечными пределами определяется формулой: 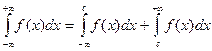 , где с – произвольное число. В этом случае интеграл сходиться лишь тогда, когда сходятся оба интеграла справа.
, где с – произвольное число. В этом случае интеграл сходиться лишь тогда, когда сходятся оба интеграла справа.
Пример.
Вычислить несобственный интеграл 


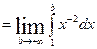 =
=