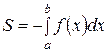Определённый интеграл от неотрицательной функции y=f(x) на отрезке [a;b] численно равен площади криволинейной трапеции:
 .
.
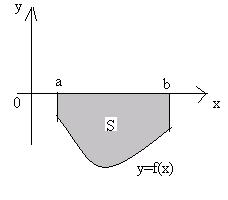
Если f(x) < 0 во всех точках промежутка [a;b] и непрерывна на этом промежутке (например, как изображено на рисунке), то площадь криволинейной трапеции, ограниченной отрезком [a;b] горизонтальной оси координат, прямыми x = a; x = b и графиком функции y = f(x), определяется формулой.