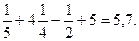Пусть на промежутке [a;b] задана непрерывная и неотрицательная функция y=f(x). Требуется найти площадь S криволинейной трапеции, т. е. фигуры, ограниченной графиком этой функции, отрезком [a;b] оси Оx и прямыми x=a и x=b(см. рис.1).
Если F(x)-некоторая первообразная для функции f(x) на интервале [a;b], то S=F(b)-F(a). Величина F(b)-F(a) называется определенным интегралом от a до b функции f(x) и записывается следующим образом:
= F(b)-F(a)= 
- формула Ньютона-Лейбница, где число a -нижний предел, а число b ¾ верхний предел интегрирования.
Cвойства определенного интеграла:
1. 
(здесь k ‑ произвольное число);
2. 
;
3. 
;
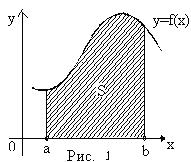
4. Если cÎ[a;b] (см. рис. 2), то 
.
Из этих свойств следует, например, что 
.
Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.
Пример.
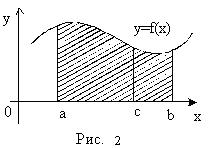
Вычислить определенный интеграл: 
.
Решение. = 
