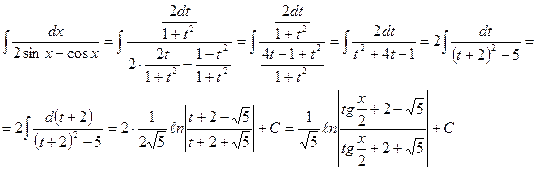Формулы тригонометрии позволяют перейти от интегрирования произведения тригонометрических функций к интегрированию суммы или разности тех же функций.
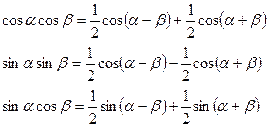
Пример 1: Вычислить интеграл 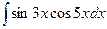
Решение:
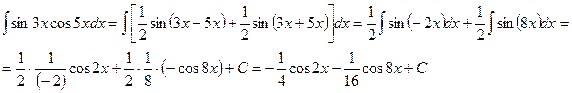
Вычисление интегралов вида  , где m или n - нечетное число
, где m или n - нечетное число
Если m - нечетное, то следует использовать подстановку  .
.
Если n - нечетное, то следует использовать подстановку  .
.
Пример 2: Вычислить интеграл 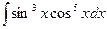
Решение:
Отделяем от одной из нечетных степеней (низшей) один множитель,  и заменяем
и заменяем  , тогда
, тогда  или
или  .
.
В итоге получаем
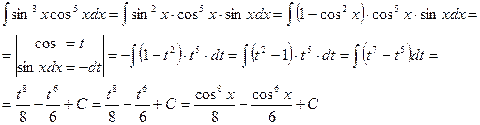
Вычисление интегралов вида  , где m и n -четное числа
, где m и n -четное числа
Использовать тригонометрические формулы понижения степени:
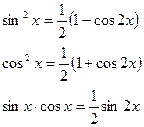
Пример 3: Вычислить интеграл 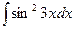
Решение:
Используя формулу понижения степени  , получаем
, получаем
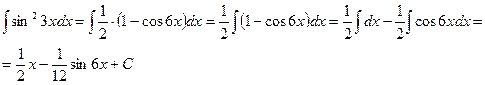
Вычисление интегралов вида 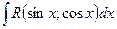
Под интегралом вида 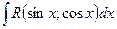 понимается интеграл, содержащий дробь, элементами которой являются тригонометрические функции, например,
понимается интеграл, содержащий дробь, элементами которой являются тригонометрические функции, например,
В таких случаях используется универсальная тригонометрическая подстановка.
Данная подстановка интеграл от любой рациональной относительно 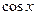 и
и  тригонометрической функции приводит к интегралу от рациональной функции.
тригонометрической функции приводит к интегралу от рациональной функции.
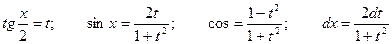
Пример 4: Вычислить интеграл 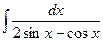
Решение:
Полагая  и заменяя
и заменяя  ,
, 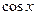 и
и  указанными выражениями через t, получаем
указанными выражениями через t, получаем