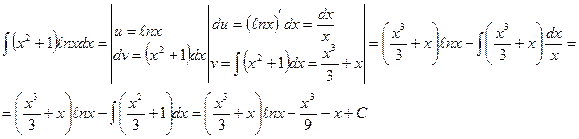При интегрировании функций, содержащих произведения, логарифмы и обратные тригонометрические функции, удобно использовать способ интегрирования по частям.
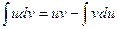
При практическом использовании формулы интегрирования по частям данное подынтегральное выражение представляют в виде произведения двух сомножителей, которые обозначают через u и 
. При этом за u берется такая функция, которая при дифференцировании упрощается, а за - та часть подынтегрального выражения, интеграл от которой легко вычисляется.
Обычно интегрированием по частям вычисляются интегралы следующих видов.
В случае интегралов вида 
, 
, 
в качестве u следует принять 
, а за соответственно выражения 
.
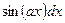
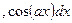В случае интегралов вида 
, 
в качестве u следует принять соответственно функции 
, а за выражение 
.
Пример 19.1:Вычислить интеграл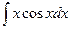 
Решение:
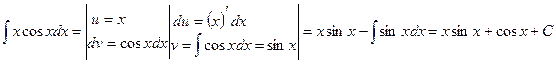
Пример 19.2:Вычислить интеграл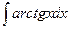 
Решение:
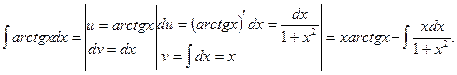
Для вычисления полученного в правой части равенства интеграла можно использовать замену переменной:
.
В результате получаем окончательный ответ:
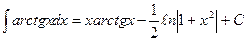
Пример 19.3:Вычислить интеграл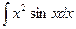 
Решение:
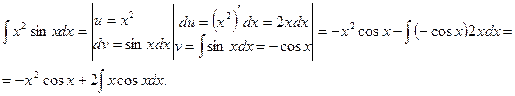
Для нахождения полученного в правой части равенства интеграла снова интегрируем по частям:
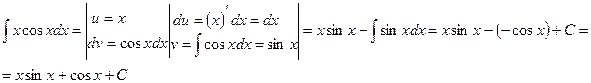
В результате получаем окончательный ответ:
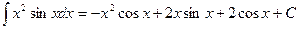
Пример 19.4:Вычислить интеграл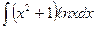 
Решение:
