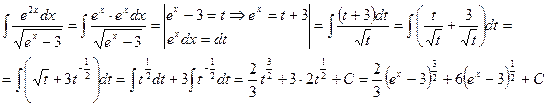Если заданный интеграл с помощью алгебраических преобразований трудно или невозможно свести к одному или нескольким табличным интегралам, то для его отыскания применяют особые способы, одним из которых является способ подстановки (замены переменной).
Способ подстановки заключается в следующем: новой переменной заменяют такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя, который всегда можно вынести за интеграл).
.
Выбор удачной формулы (подстановки) для замены переменной имеет большое значение. Вместе с тем дать одно общее правило для выбора хорошей подстановки невозможно. Однако можно посоветовать в качестве потенциальной подстановки рассматривать наиболее сложную часть подынтегральной функции.
Пример 18.1:Найти интеграл 
.
Решение:
Полагаем 
; дифференцируя обе части, получаем 
. Далее подставляем эти выражения в исходный интеграл и возвращаемся к заданной переменной x.
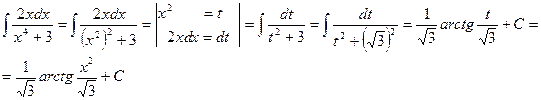
Пример 18.2:Найти интеграл 
.
Решение:
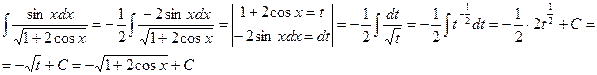
Пример 18.3:Найти интеграл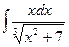 
.
Решение:
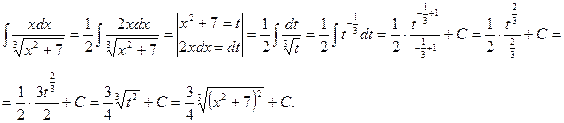
Пример 18.4:Найти интеграл 
.
Решение:
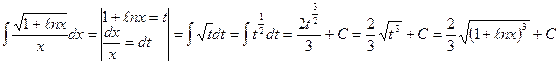
Пример 18.5:Найти интеграл 
.
Решение:
