Определение. Запись числа z в виде z= 
называется алгебраической формой комплексного числа.
Определение. Соотношения между модулем и аргументом комплексного числа z и его действительной и мнимой частями устанавливаются формулами: 
; 
. Заменяя x и y в записи комплексного числа z= их выражениями через r и 
, получаем тригонометрическую форму комплексного числа: 
, где 
= 
-модуль, =аrg z- главное значение аргумента.
Определение. Запись числа z в виде 
, где = 
, =аrg z называется показательной формой комплексного числа.
Пример 17.4
Записать комплексное число z= 
в тригонометрической и показательной форме.
Решение.
= 
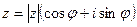
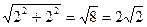-модуль комплексного числа
аrgz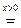 
-главное значение аргумента.
- тригонометрическая форма комплексного числа z= .
z= 
- показательная форма комплексного числа z= .
Ответ: , z= .
Формула для возведения комплексного числа в натуральную степень n (формула Муавра): 
.
Пример 17.5
Найти 
.
Решение.
Запишем данное комплексное число в тригонометрической форме: -1+i= 
. По формуле Муавра: = 
=
=1024 
=1024(-1+0i)=1024.
Ответ: 1024.
Извлечение корня из комплексного числа: 
, где k=0, 1, 2, …, n-1.
Пример 17.6
Найти 
.
Решение.
Запишем данное комплексное число в тригонометрической форме: -1+i= .
По формуле извлечения корня из комплексного числа:
, k=0, 1, 2, откуда получаем три значения корня:
при k=0: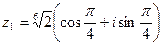 
при k=1: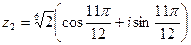 
при k=2: 
.
