Определение.Комплексными числами называются числа вида z= 
, где x, y-действительные числа, i-мнимая единица, определяемая равенством 
. Действительные числа x и y называются соответственно действительной x=Re z и мнимой y=Im z частями комплексного числа z.
Пример 17.1
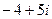Приведем примеры комплексных чисел: z= 
, z=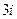 
, z= 
, z= 
.
Действия над комплексными числами
Пусть 
и 
, тогда
1. 
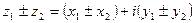
2. 
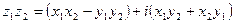
3. 
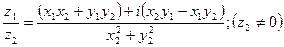
Пример 17.2
Даны комплексные числа z1= , z2= 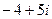. Найти 
, 
, 
.
Решение.
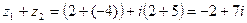
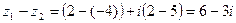
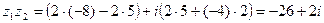
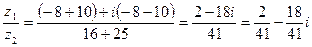
Определение.Геометрически каждое комплексное число z= изображается точкой M(x;y) координатной плоскости xOy (рис.17.1). В этом случае плоскость xOy называют комплексной числовой плоскостью, или плоскостью комплексного переменного z.
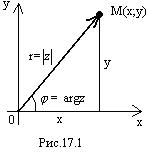
Определение.Полярные координаты r= 
= 
и 
=аrg z точки М называются модулем и аргументом комплексного числа z.
Определение.Значение угла , которое удовлетворяет неравенству 
, называют главным значением аргумента z и обозначают argz.
Аргумент z можно определить по формуле:
аrgz=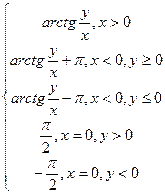 
Пример 17.3
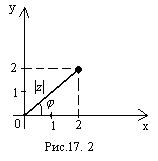
Изобразить комплексное число z= на комплексной числовой плоскости, найти его модуль и главное значение аргумента.
Решение.
Изобразим z= на комплексной числовой плоскости; х=2 и y=2 (рис.17.2).
Найдем модуль = , так как х=2 и y=2, тогда = 
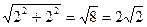
Найдем главное значение аргумента: аrgz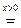 
.
Ответ: = 
, аrgz= 
.
