Определение. Пусть функция f(x) имеет производную в каждой точке промежутка (a;b). Если на промежутке (a;b) график функции f(x) расположен выше любой своей касательной, проведенной в точке этого промежутка, то функция называется выпуклой внизна этом промежутке (рис. 16 (в)).
Определение. Если на промежутке (a;b) график функции f(x) расположен ниже любой своей касательной, проведенной в точке этого промежутка, то функция называется выпуклой вверх на этом промежутке (рис. 16(г)).
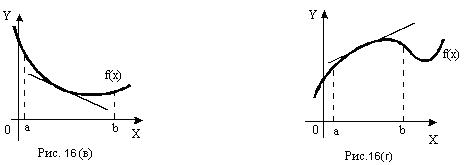
Определение.Точка x0 называется точкой перегибаграфика непрерывной функции f(x), если она разделяет интервалы, в которых функция выпукла вниз и вверх (рис. 16(д)). Угловая точка не является точкой перегиба (рис.16(е)).

Теорема 15.2. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то она выпукла вниз (выпукла вверх) на этом промежутке.
Пример 16.2
Найти интервалы выпуклости и точки перегиба функции y=  .
.
Решение.
D(y)=R
Имеем 
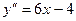
6x-4=0  x=
x= 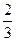
| x
| (  , , 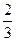 ) )
| 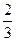
| ( 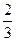 , ,  ) )
|

| +
| т. перегиба
| ¾
|
| y
| È
| 1,6
| Ç
|
Ответ: функция выпукла вниз на интервале (  ,
, 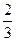 ) и выпукла вверх на интервале (
) и выпукла вверх на интервале ( 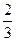 ,
,  ), точка x=
), точка x= 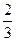 - точка перегиба функции y=
- точка перегиба функции y=  .
.