Возрастание и убывание функций, экстремумы функций

Определение.Функция y=f(x) называется возрастающей (убывающей) на промежутке X, если для любых верно неравенство .

Теорема 16.1. Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то она возрастает (убывает) на этом промежутке.

Точки области определения функции, в которых производная либо равна нулю, либо не существует, называются критическими.

Определение.Точка x₀ называется точкой минимумафункции f(x), если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие: f(x) > f(x₀) (рис 16(а)).

Определение. Точка x₀ называется точкой максимума функции f(x), если можно найти такую окрестность этой точки, что для любой точки x из этой окрестности выполняется условие: f(x) < f(x₀) (рис.16(б)).

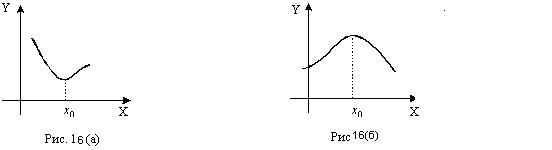
Определение. Точки максимума и минимума функции называются точками экстремума.

Пример 16.1

Найти интервалы монотонности и экстремумы функции y= .

Решение.

D(y)=R

Имеем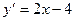

; x=2 -критическая точка

x	( ,2)		(2, )
	¾	min	+
y	¯	-1	­

Ответ: функция убывает на интервале ( ,2) и возрастает на интервале (2, ), точка x=2 - минимум функции y= .