Четность, нечетность функции
Для того, чтобы определить четность функции сперва необходимо найти область определения функции, если оно - симметричное множество, то функция либо четная либо нечетная, если же не симметричное множество, то данная функция общего вида.
Определение. Функция y=f(x) называется
четной, если выполняется условие: f(-x)= f(x),
нечетной, если f(-x)= -f(x),
общего вида, если f(-x) 
f(x) и f(-x) -f(x).
График четной функции симметричен относительно оси ординат Оy, а нечетной функции - относительно начала координат.
Пример 10.3
1. y=tg(cosx)
D(f)=(- 
;+ )-симметричное множество, следовательно проверим условия четности.
y(-x)=tg(cos(-x))=tg(cos(x))=y(x) 
данная функция четная.
2. Y=sinx
D(f)=(- ;+ )-симметричное множество, следовательно проверим условия четности.
y(-x)=sin(-x)=-sinx= -y(x) данная функция нечетная.
3. y=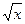 
D(f)=[0;+ )- несимметричное множество, следовательно данная функция общего вида.
