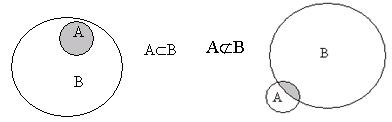Понятие множества в математике вводится на основе представления о совокупностях, образованных из конечного или бесконечного числа объектов, называемых элементами множества. Множество, не содержащее ни одного элемента, называется пустыми обозначается: Æ. Множества обозначаются большими прописными буквами латинского алфавита A, B, C…X, Y, Z, а их элементы малыми буквами a, b, c…x, y, z.
Порядком множества называется число его элементов; множество бесконечного порядка называется бесконечным (N-бесконечно). Бесконечное множество называется счетным, если его элементы можно пронумеровать. Множество чисел N,Z - счетные, множества чисел R,C-несчетные.
Множества задаются перечислением своих элементов, например, запись X=íxÎ R ½-2<3x-1<5ý означает, что множество X состоит из всех действительных чисел, удовлетворяющих указанному двойному неравенству.
Множество А называется подмножеством множества В, если любой элемент множества А принадлежит множеству В и обозначается: АÌВ.
Для иллюстрации множеств удобно пользоваться диаграммами Венна (кругами Эйлера), в которых элементы множеств схематически изображаются точками некоторых кругов.
Примеры 9.1