Код Грея не базируется на системах счисления и применяется в технике аналого-кодового преобразования, где он позволяет свести к единице младшего разряда погрешность неоднозначности при считывании. Достигается это за счет того, что смежные числа этого кода отличаются только в одном разряде. Комбинации кода Грея, соответствующие десятичным числам от 0 до 15, приведены в таблице 2.1.
Таблица 2.1
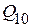
| Код Грея
| 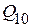
| Код Грея
| 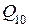
| Код Грея
|
|
|
|
|
|
|
|
Формируются комбинации кода Грея из обычного двоичного кода путем суммирования по модулю 2 исходной кодовой комбинации с такой же комбинацией, сдвинутой вправо на 1 разряд. Младший разряд в сдвинутой комбинации при этом отбрасывается.
Пример:
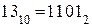
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| – код Грея
|
Перевод числа из кода Грея в обычный двоичный осуществляется по следующему правилу: все предшествующие нули и первая единица со стороны старших разрядов остаются без изменения; последующие символы (0 и 1) остаются без изменения, если число единиц, им предшествующих в коде Грея, четно, и инвертируются, если число единиц нечетно.
Пример:
|
|
|
|
|
|
|
|
| – код Грея
|
|
|
|
|
|
|
|
|
| – двоичный код
|
Проверка:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| – код Грея
|