Многочлены Безье
Кубический сплайн
Пусть на отрезке [a,b] задана сетка:
a ≤ x1 ≤…≤ xn ≤ b
a ≤ y1 ≤…≤ yn ≤ b
Аппроксимируем на каждом отрезке I данной сетки кубический полином вида:
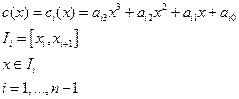
При этом необходимо чтобы выполнить следующее условие:
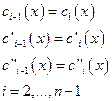
+2 условие, которое должно выполняться
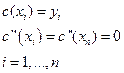
Тогда в аналитическом виде можно записать:
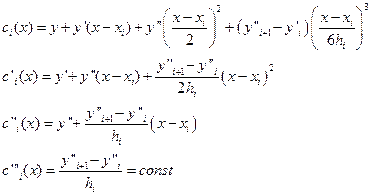
Вычисляется методом прогонки.
Задаются в параметрической форме в следующем виде:
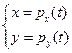
Пусть дан набор точек:
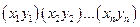
Данный набор точек называется ориентирами, тогда соответствующий многочлен Безье будет иметь вид:
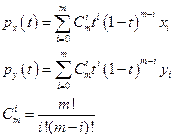
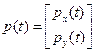
Тогда в матричном ви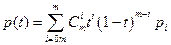де:
, где
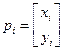
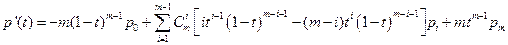
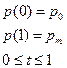
При числе m > 5 для нахождения членов Безье более эффективна схема Горнера.
Свойства кривых Безье:
1. Кривая, порождаемая многогранником Безье, обладает следующими свойством:
Любую дугу входящую в нее также можно породить с помощью многочленов Безье
2. При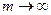 
кривая Безье 
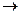к многограннику
Поверхность – непрерывное двухпараметрическое множество точек.
Поверхность считается заданной, если относительно любой точки пространства можно однозначно и сколь угодно точно решить вопрос о ее принадлежности к данной поверхности.
Поверхность может быть математически представлена в явном виде:
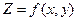
В неявном виде:
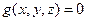
В параметрической форме:
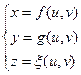
В векторной форме:
В матричной форме и других видах задания поверхности.
