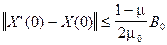Единственность решения
Быстрота сходимости процесса Ньютона
Теорема о существовании корней и сходимости процесса Ньютона
Пусть дана нелинейная система уравнений
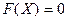 ,
,
где  - вектор-функция определена и непрерывна вместе со своими частными производными первого и второго порядков в некоторой области
- вектор-функция определена и непрерывна вместе со своими частными производными первого и второго порядков в некоторой области  . Положим, что
. Положим, что 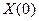 - есть точка, лежащая в
- есть точка, лежащая в  вместе со своей замкнутой
вместе со своей замкнутой 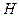 -окрестностью. При этом выполняются следующие условия:
-окрестностью. При этом выполняются следующие условия:
1) матрица Якоби при 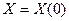 имеет обратную функцию
имеет обратную функцию

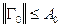
2) 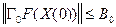
3) 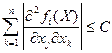
4) постоянные 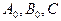 удовлетворяют неравенству
удовлетворяют неравенству
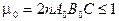
Тогда процесс Ньютона при начальном приблежении 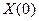 сходится к решению
сходится к решению 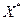 - есть решение такое, что
- есть решение такое, что 
Для проверки условия 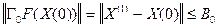 даёт оценку расходимости начального и первого приблежения.
даёт оценку расходимости начального и первого приблежения.
Если выполнимы все четыре условия теоремы 1, то для последовательных приближений 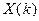 ,
,  справедливо неравенство:
справедливо неравенство:

где  - искомое решение, а
- искомое решение, а 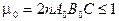
При  сходимость метода - сверхбыстрая.
сходимость метода - сверхбыстрая.
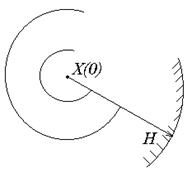
Если выполнимы все четыре условия, в области
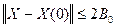
то содержится единственное решение системы
Если выполнимы все четыре условия и 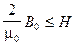 , то процесс сходится к единственному решению
, то процесс сходится к единственному решению  в основной области
в основной области 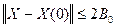 при любом выборе начального условия из области
при любом выборе начального условия из области