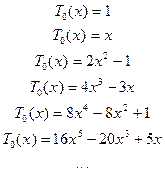Интерполяция сплайками
Погрешность формулы Ньютона для неравностоящих узлов
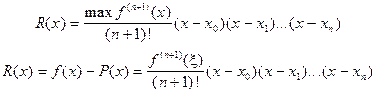
где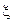 
- промежуточное значение между точками 
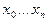и 
Даны: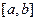 
, разбитый на разные отрезки с узлами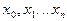 
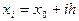
и соответствующие им значения функции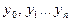 
Сплайком называется функция, которая вместе с несколькими производными непрерывна на заданном отрезке 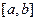, и на каждом частичном отрезке 
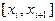в отдельности является некоторым алгебраическим многочленом, причём степени многочлена различны.
Степень сплайка - максимальная степень многочлена.
Дефект сплайка - разность между степенью сплайка и порядком наивысшей производной на отрезке .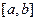
На практике широкое применение получили кубические сплайки.
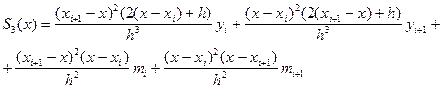
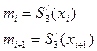
Таким образом для интерполяции сплайками, необходимо знать не только значения функции в точках 
и 
; а ещё и их производные
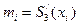- наклон сплайка
Как задаётся наклон сплайка?
1. Упрощённый способ
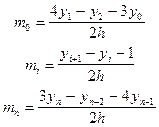
2. Если известны значения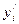 
=> 
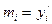
3. Глобальный
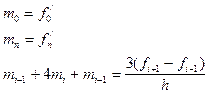
Сплайки являются наиболее удобным средством апроксимации функций на небольших промежутках, то есть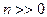 
.
При апрксимации функций интерполяционными многочленами можно потребовать очень высокой степени полиномы, тогда как разбиения на участки, содержащих несколько участков, правда при этом в савке двух многочленов первая производная терпит разрыв.
Особенность интерполяции функции многочленами Чебышева заключается в том, что приведённые многочлены минимизируют максимальную погрешность 
