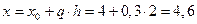Выбор узлов интерполирования
На практике ИФН обрывается на членах, содержащих разности в пределах заданной точности. В этом случае остаточный член да 2инф:
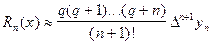 - 2ИФН (1)
- 2ИФН (1)
 - 1ИФН (2)
- 1ИФН (2)
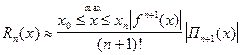 - Лагранж (3)
- Лагранж (3)

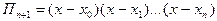
Анализируя погрешности интерполяционных формул, можно сделать следующий вывод:
1. Остаточные члены зависят от выбора узлов интерполирования:
(1) и (2) = 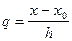
(2) 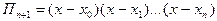
2. В первых двух формулах видоизменить что-либо сложно, ибо само условие означает равноотстоящие узлы.
3. В формуле Лагранжа можно выбирать узлы. При неудачном выборе узлов интерполирования погрешность 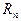 может быть очень большой.
может быть очень большой.
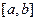 если сконцетрировать около одного из концов, то
если сконцетрировать около одного из концов, то 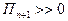
Рациональный вывод узлов, чтобы полином 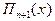 имел наименьшее максимальное значение по абсолютной величине на отрезке
имел наименьшее максимальное значение по абсолютной величине на отрезке 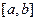 => “наименее отклонился от шрся на
=> “наименее отклонился от шрся на 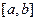 .
.
Эта задача решима русским математиком Чебышевым

где 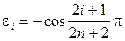 ,
, 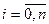 => это узлы Полином Чебышева
=> это узлы Полином Чебышева 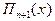
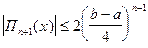
Эти узлы неравноотстоящие, а сгущаются около концов отрезка.
Задача обратного интерполирования заключается в том, чтобы по функции 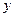 найти значение аргумента
найти значение аргумента  .
.
Предположим, что  монотонна и значение
монотонна и значение 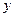 содержится между
содержится между 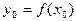 и
и 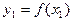 . Заменяя
. Заменяя 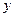 интерполяционным полиномом Ньютона, имеем:
интерполяционным полиномом Ньютона, имеем:
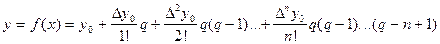
ð 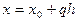 , где
, где 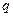 число шагов, необходимых для достижения точки
число шагов, необходимых для достижения точки  , исходя из точки
, исходя из точки 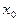 .
.
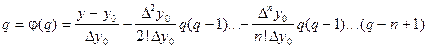
За начальное приближение принимаем:
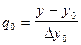
Применяя метод итерации, получим:
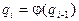
Итерационный процесс, останавливается, когда
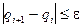 и тогда
и тогда  =>
=> 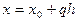
Пример:
Задано 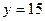 . Определить
. Определить  с точностью
с точностью 
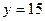
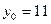
Горизонтальная таблица разностей:
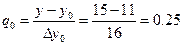

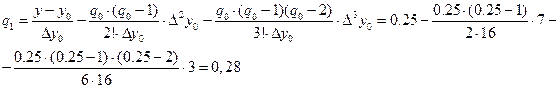
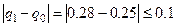 Þ
Þ 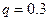
Тогда