Интерполяционная формула Лагранжа.
Пусть на отрезке [a;b] даны n+1 различных значений аргумента x: x0, x1,…, xn и известны соответствующие их значению функции y=f(x) : f(x0)=y0, f(x1)=y1, f(xn)=yn. Требуется построить полином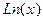 
степени не выше 
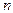, имеющий в заданных узлах 
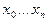те же значения, что и функция 
, т.е. Ln(xi)=yi при i=1,n
;
,
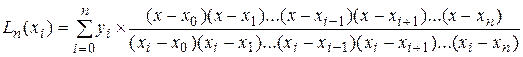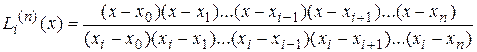где Li(n)- коэффициенты Лагранжа.
Следует отметить, если узлы равностоящие, то интерполяционный полином Лагранжа совпадает с интерполяционной формулой Ньютона.
Примечательно то, что формула Лагранжа зависит лишь от yi, а не от разностей.
n=1
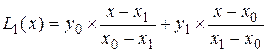
При n=1 имеем 2 точки: (x0;y0) и (x1;y1).
прямая, проходящая через эти точки-
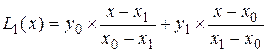
n=2 (x0;y0), (x1;y1), (x2;y2)
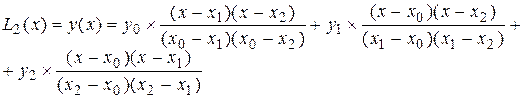Пример:
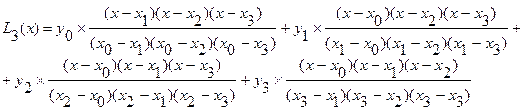L3(x)=x3+x2-x+2
Для вычисления лагранжевых подмножеств удобно составлять следующую таблицу разности:
| x-x0
| x0-x1
| x0-x2
| …..
| x0-xn
|
| x1-x0
| x-x1
| x1-x2
| …..
| x1-xn
|
| x2-x0
| x2-x1
| x-x2
| …..
| x2-x1
|
| …..
| …..
| …..
| …..
| …..
|
| xn-x0
| xn-x1
| xn-x2
| …..
| x-xn
|
Обозначим произведение элементов i-ой строки через Di , а произведение главной диагонали Пn+1(x). Отсюда следует, что:
Пn+1(x)=(x-x0)(x-x1)…(x-xn)
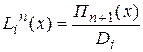при i=1,n
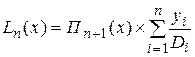
Для упрощения вычислений можно использовать инвариантность (при равноотстоящих точках лагранжевых коэффициентов),если
x= at+b
xj= atj+b при j=0,n
то Li(n)(x)= Li(n)(t)
