Для определения степени нечёткости множества введено понятие меры нечёткости, сводящейся к измерению уровня различия между множеством 
и его отрицанием 
.
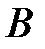Наиболее популярной является мера Р. Егера, в соответствии с которой степень нечёткости множества в метрике 
, обозначаемая 
, определяется выражением [6]:
, (8.31)
где 
- это мера расстояния между множествами и 
, содержащими 
элементов. Значение 
соответствует метрике Хемминга, в которой:
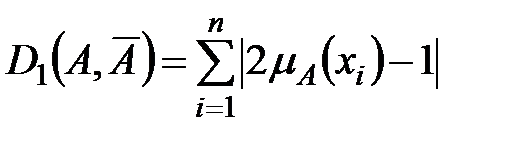, (8.32)
а значение 
соответствует метрике Евклида, в которой:
. (8.33)
Пример 8.2.
Если нечёткое множество определяется дискретным способом как:
, то принимая во внимание, что
, в соответствии с мерой Егера получаем:
,
.
Другую меру нечёткости предложил Б. Коско [4]. Она основана на понятии кардинального числа множества. В соответствии с этой мерой:
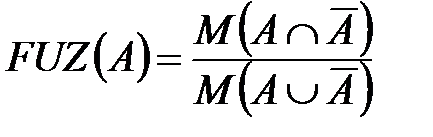, (8.34)
где 
обозначает кардинальное число множества 
. Для множества из примера 8.2 получаем меру Коско, равную:
.
Следует обратить внимание, что обе меры для чётких множеств дают один и тот же нулевой результат, так как в мере Коско 
, а 
, что вследствие зависимости (8.14) даёт в результате также 
.
