Рассмотрим систему n линейных уравнений с n неизвестными:
или АХ=В (П1.3.1)
Обозначим D=det A.
Dj= 
,
т. е. Dj – определитель матрицы, полученной из А заменой столбца Аj на столбец В свободных членов.
Докажем для i= 
справедливость тождества
, i= . (П1.3.2)
Имеем:
+ 
+...+ 
+...=
i-й столбец
Разлагая каждый определитель по столбцу В, и приводя подобные относительно bk, k= 
, получим
| как определители матриц с двумя одинаковыми строками
| |
= 
+
+ ...
+ 
+ 
= 
.
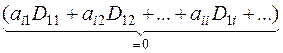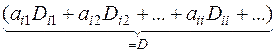Если 
, то (П1.3.2) можно разделить на D, получив
, i= 
; то есть, для j=
– решение системы
Получен нижеследующий результат:
Если detA 
0 и решение системы (П1.3.1) существует,
то оно может быть получено по формулам Крамера:
, j=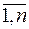 
.
