1. Закон дополнительных элементов:
х+х=1
х*х=0
2. Двойное отрицание:
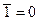
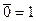
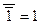
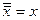
Выражения этих законов широко используется для минимизации логических схем. Если удаётся выделить из общего выражения логической функции такие подвыражения, то можно сократить необходимое количество входов элементов цифровой схемы, а иногда и вообще свести всё выражение к логической константе.
3. Закон отрицательной логики:
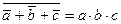
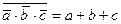
Закон отрицательной логики справедлив для любого числа переменных. Этот закон позволяет реализовывать логическую функцию "И" при помощи логических элементов "ИЛИ "и наоборот: реализовывать логическую функцию "ИЛИ" при помощи логических элементов "И". Это особенно полезно в ТТЛ схемотехнике, так как там легко реализовать логические элементы "И", но при этом достаточно сложно реализуются логические элементы "ИЛИ". Благодаря закону отрицательной логики можно достаточно просто реализовывать элементы "ИЛИ" на логических элементах "И". На рисунке 6.3 показана реализация логического элемента "2ИЛИ" на элементе "2И-НЕ" и двух инверторах.
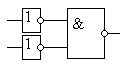
Рисунок 6.3 – Логический элемент "2ИЛИ", реализованный
на элементе "2И-НЕ"
То же самое можно сказать и о схеме монтажного "ИЛИ". В случае необходимости его можно превратить в монтажное "И", применив инверторы на входе и выходе этой схемы.