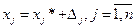Текущий и окончательный контроль вычислений в методе Гаусса
Для контроля вычислений параллельно системой 
решается система 
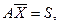где S – вектор.
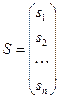
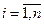
Если над числами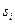 
выполнять те же действия, что и над числами 
, то на любом этапе схемы единственного деления и схемы Жордана сумма коэффициентов строки и свободного члена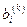 
должна давать числа 
. Это и есть текущий или построчный контроль вычислений. Если эти числа отличаются существенно, а не на одну - две единицы последнего разряда, то в строке допущена ошибка и коэффициенты следует пересчитать.
Эта же система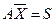 
служит и для окончательного контроля вычислений.
Если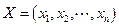 
есть решения системы , то решением системы 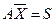будет вектор 
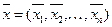такой, что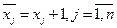 
Доказательство: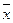 
подставим в левую часть уравнения 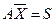, будем иметь
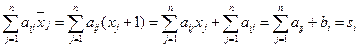
Таким образом, окончательный контроль заключается в том, что решения систем и 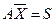должны отличатся на единицу.
Решение, получаемое по методу Гаусса, является приближенным, то есть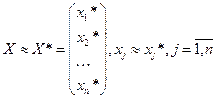 
Решение 
можно уточнить.
Если подставить в уравнение (1’), получим приближенное равенство.
Разность 
называют невязкой.
Так как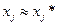 
, то 
называется поправкой 
Так как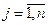 
, то получаем вектор поправок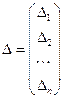 
Подставим вектор X в систему ( 2 )
вектор невязок
Решение новой системы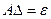 
с той же матрицей коэффициентов, но с другой правой частью дает вектор поправок.
и можно получить уточненное решение: 
