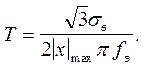Восстановление по непрерывного сигнала по теореме Котельникова связано с задержкой сигнала, что неприемлемо в системах работающих в реальном масштабе времени.
Для восстановления сигнала в реальном масштабе времени необходимы способы восстановления с экстраполяцией (предсказанием) сигнала. При этом могут использоваться полиномы различной степени. Простейший полином - 0-й степени. Рассмотрим этот случай (рис. 4.4.).
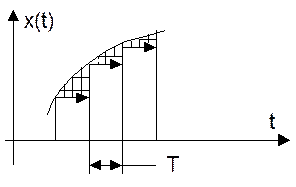
Рис. 4.4.
Требуется определить интервал времени Т, при котором погрешность восстановления не превышает допустимых пределов, т.е. sв £ (sв)допуст.
Для этого необходимо знать:
1. Наибольшее значение сигнала по модулю - êx êmax.
2. Эффективную ширину спектра сигнала fэ.
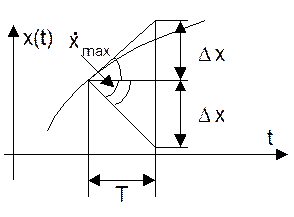
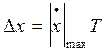, где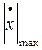 
- модуль максимальной 1-й производной от сигнала.
Для ее оценки нужно оценивать fэ. Это можно сделать с помощью неравенства Бернштейна:
x(t)= sin 2pfэt;
.
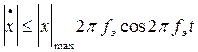При t=0 наихудшее значение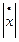 
составляет 
.
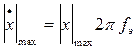С учетом неравенства Бернштейна можно получить
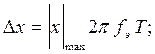
Откуда искомое значение временного интервала:
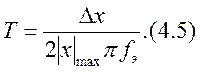
Надо на основании Dх определить sв.
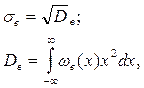
где Dв -дисперсия; wв(х) - закон распределения плотности вероятности погрешности дискретизации; х - параметр интегрирования. Рассмотрим равномерный закон распределения. В этом случае (см. раздел
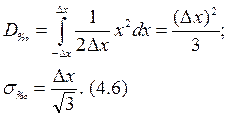
Подставляя (4.6) в (4.5) получим
