Пусть сигнал имеет вид:
,
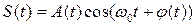где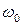 
– несущая частота, 
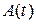и 
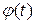– законы амплитудной и фазовой модуляции, которые задают медленно (по сравнению с 
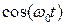) меняющиеся функции.
Если непосредственно из теоремы Котельникова выбирать частоту дискретизации, то она должна быть не меньше, чем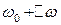 
, где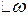 
– ширина спектра сигнала 
.
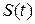Однако такой сигнал можно представить, перейдя к комплексному виду, как:
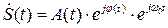
Информация, переносимая сигналом, описывается как:
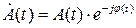
Умножим 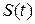на 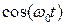в одном канале и на 
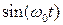– в другом (рис.4.3).:
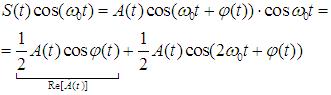
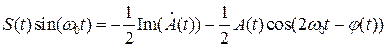
В результате получаем частоту дискретизации 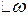. Такой принцип дискретизации называют гетеродинированием сигнала.
Рис.4.3. Принцип дискретизации с гетеродинированием сигнала
