Рассмотрим рисунок
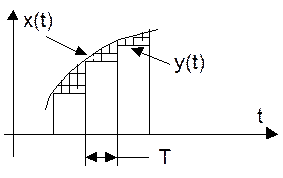
Из рисунка видно, что ошибка
e(t)=y(t)-x(t)=x(t-T)-x(t)=x(t*)-x(t*-T)=x(t)-x(t+T). Введено обозначение t*=t-T.
Дисперсия этой ошибки
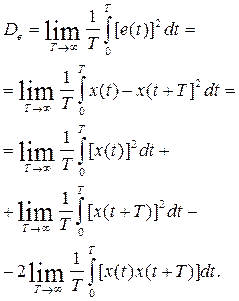
(4.7)
В выражении (4.7) первое слагаемое - Dx=Kx(0), второе слагаемое - Dx=Kx(0), третье слагаемое - 2Kx(T).
Пусть x(t) - стационарный сигнал. Он однороден во времени и его характеристики от него не зависят. Тогда
De = 2Kx(0) - 2Kx(T).
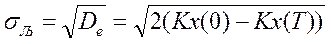. (4.8)
Методика определения шага дискретизации состоит в разрешении уравнения (4.8) относительно Т.
АКФ Кх(t) является более содержательной характеристикой, чем эффективная полоса частот. Поэтому, определение шага дискретизации по уравнению (4.8) является более точным, чем по неравенству Берншейна.
