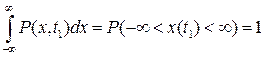Функция распределения вероятности (cumulative distribution function CDF)
(3.1)
Определить вероятность того, что в момент времени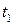 
значение случайного процесса 
не превосходит 
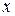
а) CDF является неубывающей функцией;
б) вероятность попадания значения случайного процесса в интервал 
:
(3.2)
Одномерная плотность вероятности (probability density function, PDF)
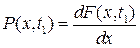(3.3)
Т.е. является производной от функции распределения и определяет характер скорость её изменения:
а) плотность вероятности является неотрицательной функцией
б) вероятность попадания 
в произвольный интервал :
(3.4)
Очевидно, что:
