Для анализа свойств случайного процесса необходимо задать математическую модель такого процесса.
Рассмотрим примеры
1. Гармонический сигнал со случайной начальной фазой
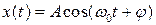
– амплитуда – известна, т.е. детерминирована
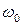– частота детерминирована
– случайная начальная фаза, принимающая любое значение на интервале 
.
При равномерном распределении такой начальной фазы на интервале 
плотность вероятности:
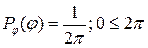
2. Случайный телеграфный сигнал
Возможны значения 
, переключение из одного состояния в другое происходит в случайные моменты времени.
Функция распределения вероятности, т.е. вероятности того, что за время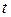 
произойдёт 
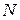переключений (случайная величина!) имеет вид:
,
где 
– параметр, определяющий среднюю частоту переключений.
Это выражение описывает закон Пуассона.
