Таблица 2.1
| Аргументы
| Функция
|
| Имеются деньги
| Необходимость есть
| Приобрести компьютер
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
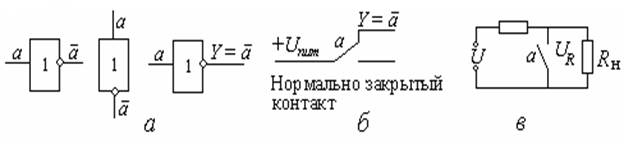
Рис. 2.1. Условное графическое обозначение (а) и релейно-контактная реализация логического элемента НЕ (б) и (в).
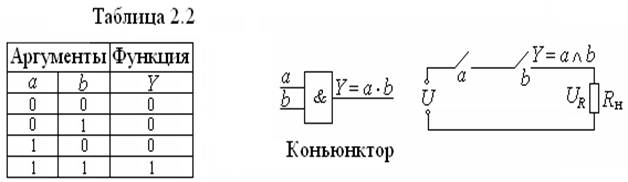
Рис. 2.2. Таблица истинности, условное обозначение и релейно-контактная реализация логического элемента И.
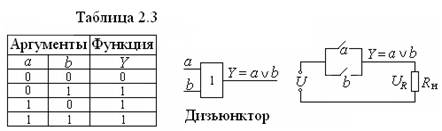
Рис. 2.3. Таблица истинности, условное обозначение и релейноконтактная реализация логического элемента ИЛИ.
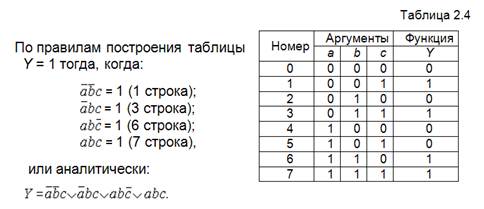
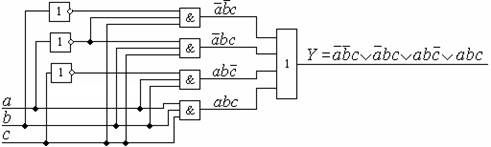
Рис. 2.4. Логическая схема, реализованная по СДНФ.
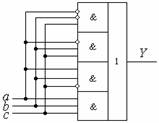
Рис. 2.5. Сокращенное условное изображение схемы по рис. 2.4
| Аксиомы операций
|
| конъюнкции
| и
| дизъюнкции
|
| 0 · 0 = 0
|
| 1 Ú 1 = 1
|
| 1 · 0 = 0 · 1 = 0
|
| 0 Ú 1 = 1Ú 0 = 1
|
| 1 · 1 = 1
|
| 0 Ú 0 = 0
|
Законы булевой алгебры
|
| Для
конъюнкции
| Для
дизъюнкции
|
| 1. Переместительный закон:
| 
| 
|
| 2. Закон повторения (тавтологии):
| 
| 
|
| 3. Закон нулевого множества:
| 
| 
|
| 4. Закон универсального множества:
| 
| 
|
| 5. Закон дополнительности:
| 
| 
|
| 6. Закон поглощения:
| 
| 
|
| 7. Закон склеивания:
| 
| 
|
| 8. Закон инверсии (закон де Моргана):
| 
| 
|
| или после инвертирования правых
и левых частей:
|
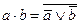
|

|
9. Закон обращения: если  , то , то 
|
10. Закон двойной инверсии: 
|
11. Сочетательный закон: 
|
12. Распределительный закон:

|
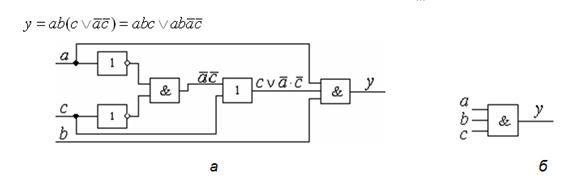
Рис. 2.6. Схемы примера: а по исходному уравнению; б после преобразования
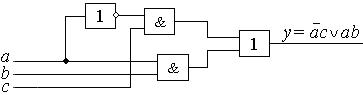
Рис. 2.7. Схема, полученная в результате минимизации уравнения (2.1)
| Таблица 2.5
| Таблица 2.6
| Таблица 2.7
|
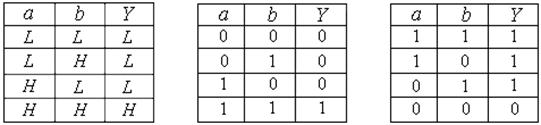
| Уровни сигналов
| Логические сигналы
| Логические сигналы
|
в положительной логике в отрицательной логике
Положительная логика Отрицательная логика
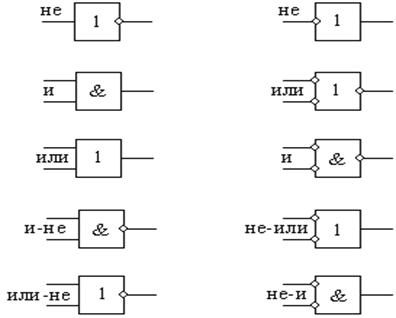
Рис. 2.8. Графическое обозначение элементов в двух видах логик