Рассмотренные схемы обладают разной степенью устойчивости. Для оценки абсолютной устойчивости схем предлагается простой способ.
В узел i-1 дополнительно к решению задается возмущение Δ1, а в узле i фиксируется реакция Δ2. Для явной схемы Эйлера можно записать(2.6).
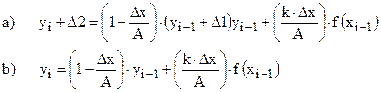
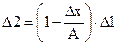(2.6)
Вычитая почленно уравнение b из уравнения a, получим выражение для относительного значения реакции ε= Δ2/ Δ1. Для явной схемы Эйлера:
(2.7)
На nом шаге от узла, где задано возмущение, (если значения A, k и Δx остаются неизменными) относительная реакция составляет εn= Δ2n/ Δ1.Для обеспечения абсолютной устойчивости разностной схемы необходимо, чтобы при n® ¥выполнялосьεn <1. А это возможно, если выполняется условие (2.8).
0 < ε < 1(2.8)
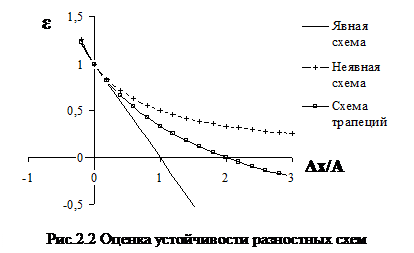Для рассмотренных разностных схем на рис.2.2 приведены графики зависимости значения ε от величины Δx/A. Видно, что неявная схема всегда устойчива, а схемы явная и трапеций имеют ограничения на величину шага:
¾ явная схема Δx/A < 1;
¾ схема трапеций Δx/A < 2.
Аналогичным образом можно оценить устойчивость различных разностных схем.
