Перспективным представляется использование единой интерполирующей функции во всей области определения табулированной функции. Чаще всего используется полиномиальная интерполяция. В этом случае для описания зависимости у = f (x) используется алгебраический многочлен (полином). Известно, что для любого набора точек (xi, yi) i=1,2,3…n существует единственный интерполяционный многочлен степени n-1
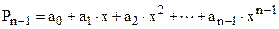, (1.4)
который проходит через все узлы интерполяции, т. е.
Для нахождения коэффициентов а0, а1, а2,…аn-1 необходимо решить систему состоящую из n линейных алгебраических уравнений вида:
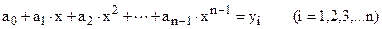. (1.5)
Следует отметить, что значение порядка полинома на единицу меньше количества заданных точек.
При использовании полиномов высоких степеней для интерполяции ряда функций возможны существенные расхождения интерполяционного и действительного значений функции в некоторых областях значений аргумента (между узлами интерполяции). В таких случаях следует использовать аппроксимацию заданного набора точек полиномом невысокого порядка.
