Аппроксимация

Приближенное выражение математических объектов через другие, более простые называют аппроксимацией.

Аппроксимация табулированной функции полиномом.

В рассматриваемом случае функциональную зависимость y=f(x) заданную таблично (табулированную) приближенно отражают (аппроксимируют) полиномом, проходящим возможно ближе к точкам с координатами (x_i, y_i), но не требуют совпадения значений искомого полинома и табулированной функции в точках (x_i, y_i). При подобной аппроксимации чаще всего используется метод наименьших квадратов.

Рассмотрим в качестве аппроксимирующей функции полином степени k

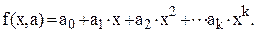(1.6)

Будем минимизировать сумму квадратов рассогласований s значений заданной и аппроксимирующей функций во всех n точках (x_i, y_i)

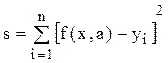. (1.7)

Согласно теории необходимым условием минимума функции s является равенство нулю ее частных производных:

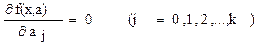. (1.8)

Развернув (1.8) получаем систему уравнений для определения a₀, a₁, a₂,…,a_k

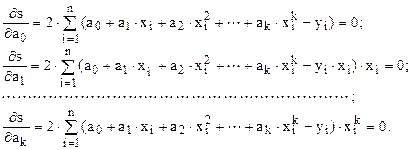(1.9)

которая приводится к системе линейных алгебраических уравнений (СЛАУ) с матрицей Грамма вида:

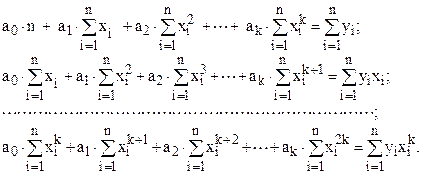(1.10)

Таким образом, для определения коэффициентов как интерполирующего, так и аппроксимирующего полиномов необходимо решить систему линейных алгебраических уравнений. Следует отметить, что многие математические модели тем или иным способом приводятся к СЛАУ и для пользователя ПЭВМ полезно ознакомиться с основными методами решения СЛАУ.