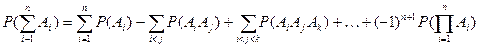Формула вероятности суммы совместных событий

(теорема сложения вероятностей)

.Пусть мы имеем два совместных события А и В. Преобразуем их сумму в сумму несовместных событий

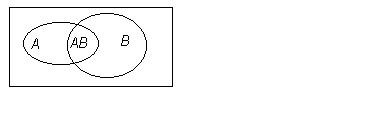
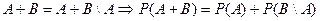
Подставляя второе выражение в первое, получим

.

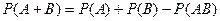Пример. По мишени один раз стреляют два стрелка. Вероятность попадания первого стрелка в мишень р₁ = 0,7, второго – р₂ = 0,8. Какова вероятность того, что кто-нибудь из них попадет в мишень?

А = А₁ + А₂, А попадание в мишень; А₁ – попал первый стрелок; А₂ – попал второй стрелок.

Р(А) =Р(А₁ + А₂)=Р(А₁)+ Р(А₂) –Р(А₁А₂)= Р(А₁)+Р(А₂) – Р(А₁ )Р(А₂)= 0.7+ 0,8 – 0,7· 0,8 = 0,94.

Получим вероятность суммы трех совместных событий.

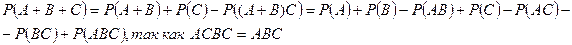
Получена формула

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС)

Обобщая полученный результат на сумму n совместных событий, получим формулу