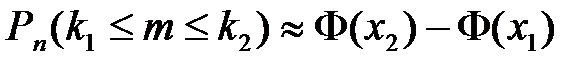,
где 
- функция Лапласа, значения которой табулированы, 
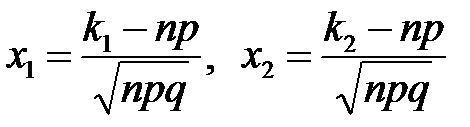
Теорема применяется в тех случаях, когда требуется вычислить вероятность, что в n независимых испытаниях событие А появится от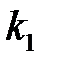 
до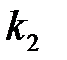 
раз включительно, при больших n и р≠0; р≠1 ( 
).
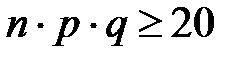Примеры.
1) Вероятность появления числительного в художественной речи равна 0, 01 [Головин, 1971, с.123]. Исследуется текст, длиной 500 знаменательных слов. Найти вероятность, что в данном тексте окажется… а) 3 числительных; б) более 3 числительных.
Решение: a) так как вероятность появления каждого числительного мала, а число слов (количество испытаний) велико, то применим формулу Пуассона. Здесь n=500, p=0,01, a=500 
0,01=5; m=3; 
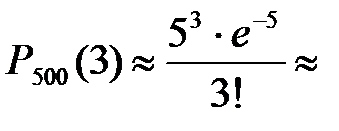0,14.
б) обозначим событие А – «в тексте более 3 числительных», тогда событие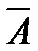 
– «в тексте не более 3 (т.е 0, 1, 2 или 3) числительных».
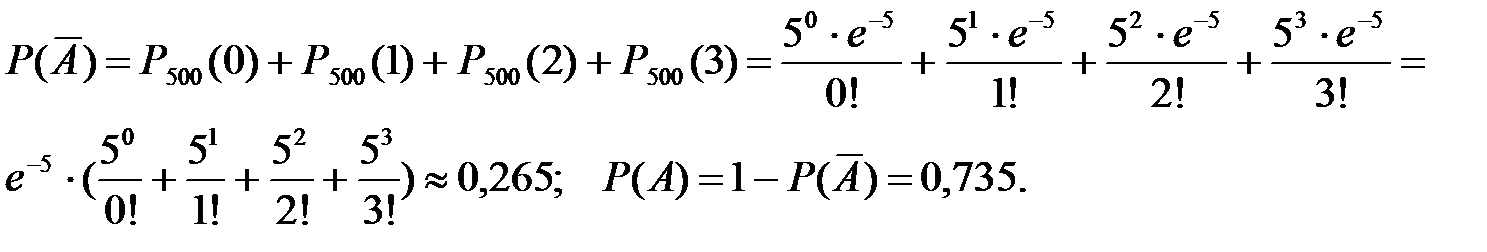2) Вероятность появления существительного в русской художественной речи равна 0,40 [Головин, 1971, с.123]. Исследуется текст, длиной 200 знаменательных слов. Найти вероятность, что в данном тексте окажется а) 70 существительных; б) от 70 до 90 существительных.
Решение: так как n – велико (n=200), а вероятность р не близка к нулю (p=0,4; q=1-p=0,6), то для нахождения искомых вероятностей используется теоремы Муавра– Лапласа: локальная и интегральная.
а)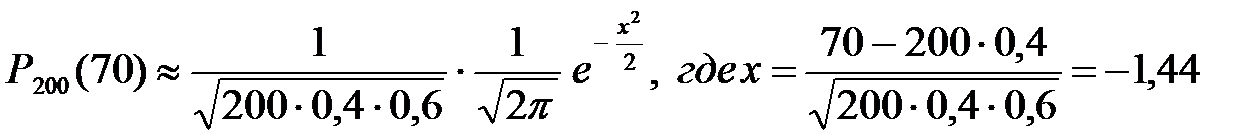 
.
Значение функции Гаусса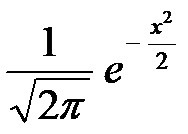 
при х=-1,44 равно 0,14 ;
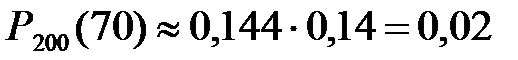
б)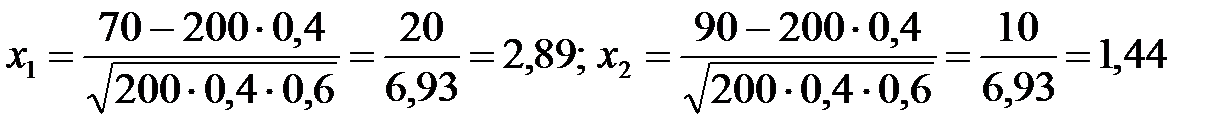 
. Φ(2,89)=0,498; Φ(1,44)=0,425; 
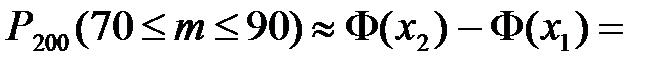0,073.
