Часто в лингвистических исследованиях приходится проводить большое число независимых испытаний n. При этом величина n может быть велика, что делает вычисление по формуле Бернулли слишком трудоёмким. В таких случаях применяют асимптотические формулы для вычисления биномиальной вероятности при n→∞.
1. Формула Пуассона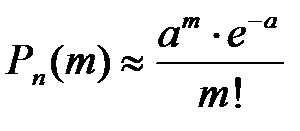 
, где параметр 
.
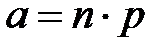Формула применяется при большом количестве испытаний n (n≥100) и малой вероятности события А р (p≤0,1). При этом а≤10.
Если количество испытаний n велико, а вероятность р не близка к нулю, то для нахождения вероятности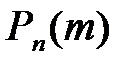 
используются теоремы Муавра - Лапласа .
2. Локальная теорема Муавра-Лапласа
,
применяется при больших n и р≠0; р≠1.
Выражение 
называется функцией Гаусса, значения которой можно найти в таблице (табулированы).
При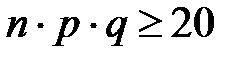 
равенство дает удовлетворительное приближение.
