Определение (квадратичной формы). Скалярная вещественная функция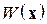 
векторного вещественного аргумента 
, 
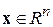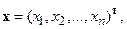называется вещественной квадратичной формой, если она определяется выражением:
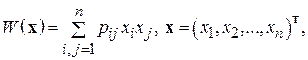(1.5.2)
причем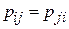 
(эти коэффициенты симметричны относительно двойного индекса),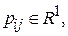 
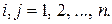
Квадратная таблица коэффициентов квадратичной формы есть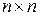 
– матрица вида
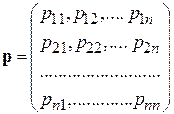, (1.5.3)
симметричная относительно главной диагонали, называется матрицей квадратичной формы (1.5.2),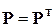 
– симметричная матрица.
Таким образом, любая вещественная квадратная симметричная числовая матрица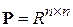 
порождает квадратичную форму вида:
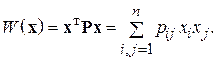(1.5.2’)
