Оси, проходящей через эту точку.

Установим зависимость между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку (рис.4.5)

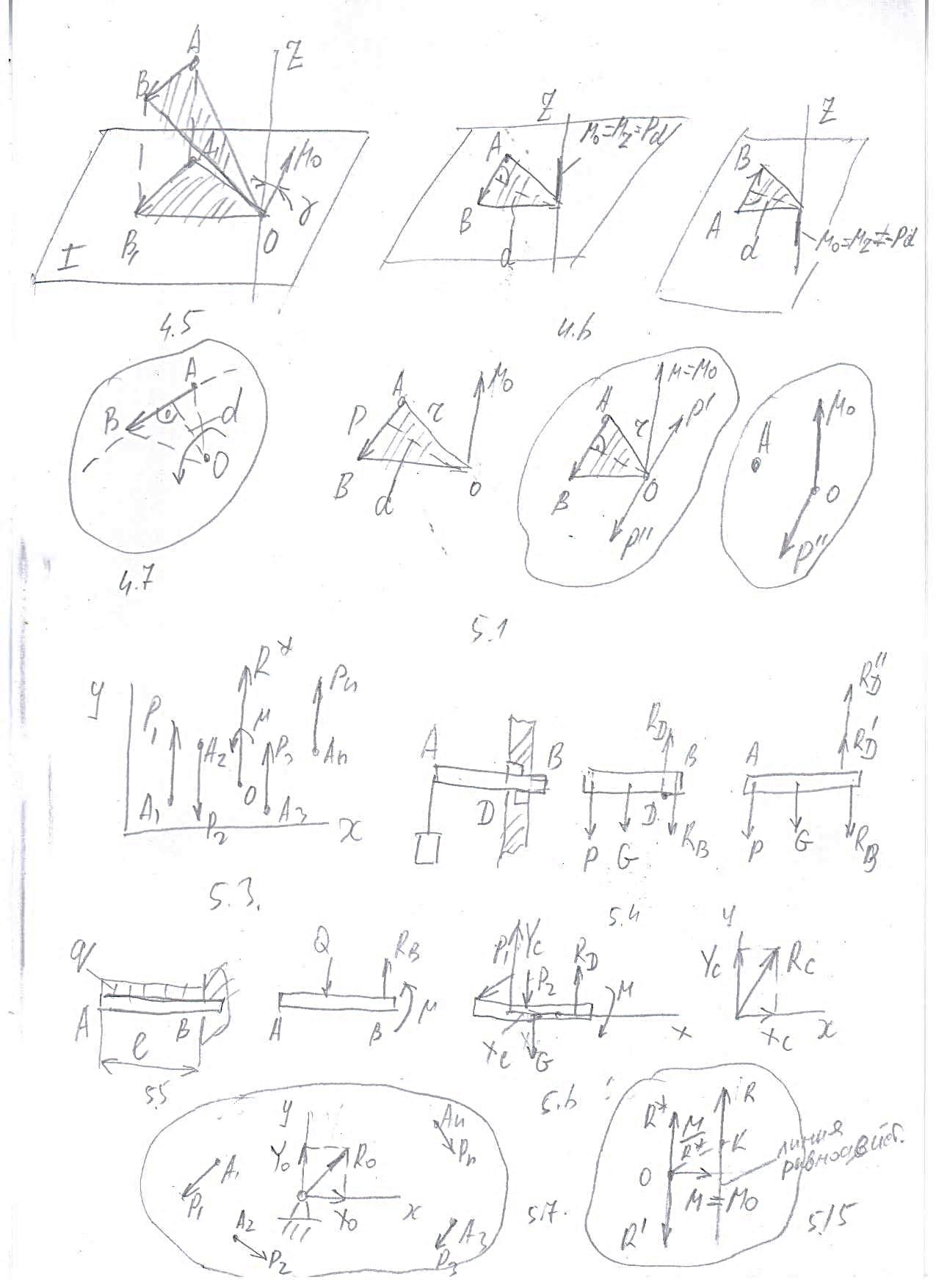
Рис. 3.5

В 3.1,3.2 установлено

Mо= 2*D АОВ; M_z= 2*D А₁ОВ₁.

Т.к. треугольник А₁ОВ₁ является проекцией треугольника АОВ на плоскость I , перпендикулярную к оси z, то его площадь равна площади треугольника АОВ, умноженной на косинус угла между этими площадями.

Известно, что угол между плоскостью треугольника АОВ и плоскостью I равен углу между перпендикулярами к этим плоскостям, т.е. углу между моментом Мо и осью z. Поэтому

пл. D АОВ*cosg= 2 пл.D А₁ ОВ₁.

Следовательно, Mo cosg= M_z или Mo cos(Мо, k) = M_z .

Проекция момента силы относительно точки на ось, проходящую через эту точку, равна моменту силы относительно этой оси.

Проекции на ось z моментов силы Р относительно различных точек оси z имеют одну и ту же величину, равную моменту силы Р относительно этой оси.

Если сила расположена в плоскости, перпендикулярной к оси, то cosg= ±1 и M_z= ±Mo.