Момент Мо силы Р относительно начала координат (см. 3.1) выражается формулой
Мо= r x P.
Разложим вектор Мо на составляющие по осям координат
Мо= iMx+ jMy+ kMz,
где Mx, My, kMz - проекции Мо на оси координат.
Векторное произведение можно представить определителем
r x P=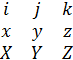 
,
где x,y,z- проекции вектора r ; X,Y,Z- проекции вектора P на оси координат.
Приравнивая значения Мо и определителя, разложенного по элементам 1-й строки, получим
iMx+ jMy+ kMz= i(yZ-zY)+ j(zX-xZ)+ k(xY-yX).
Сопоставляя левые и правые части этого равенства, находим проекции момента Мо на оси координат, равные
Mx= yZ- zY; My= zX- xZ; Mz= xY-yX. (3-1)
Формулы (3-1) называются аналитическими выражениями моментов силы относительно координатных осей.
Если имеется система сил, произвольно расположенных в пространстве и можно определить моменты всех сил относительно произвольной точки О, то построив в точке О многоугольник этих моментов можно найти их геометрическую сумму.
Момент, равный геометрической сумме моментов всех сил системы относительно точки, называется главным моментом системы сил относительно этой точки:
Мо=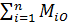 
. (3-2)
Проекция главного момента системы сил относительно некоторой точки на ось, проходящую через эту точку, равна главному моменту системы сил относительно этой оси:
Моcos(Mo,z)=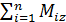 
= Mz. (3-3)
