Пусть матрица A имеет блочный вид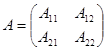 
. Припишем к ней справа единичную матрицу и найдём обратную к матрице A. Для этого выполним следующие действия:
- Умножим (слева) на матрицу
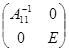(конечно в предположении существования обратной матрицы). В результате получим матрицу 
. - Вычтем из второй блочной строки первую, умноженную на матрицу
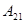(на языке матриц мы умножим слева на матрицу 
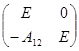). В результате получится матрица 
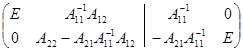. - Умножим слева на матрицу
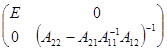. В результате получим матрицу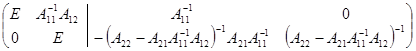 
- Вычтем из первой блочной строки вторую, умноженную на матрицу
(т.е. умножим слева на матрицу 
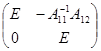). В результате получится матрица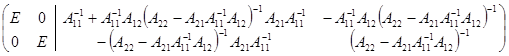 
Тем самым найдена обратная матрица к матрице A. Формула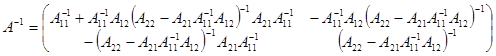 
называется формулой Фробениуса. Использование формулы Фробениуса позволяет уменьшить количество арифметических операций при вычислении обратной матрицы.
Обозначим через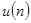 
и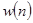 
число арифметических операций необходимых, соответственно, для обращения и умножения матриц n-го порядка. Имеет место рекуррентная формула 
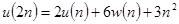. Положим 
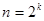, тогда при умножении матриц по формулам Штрассена 
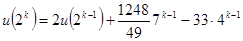. Применив формулу k раз (учитывая 
) получим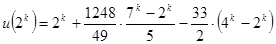 
. Подставив вместо k его выражение через n ( 
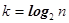) получим 
.
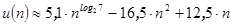