Ряд задач алгебры приводит к задаче построения решения системы линейных уравнений. Например, вычисление коэффициентов интерполяционного многочлена методом неопределённых коэффициентов. В общем виде задача отыскания решения системы линейных уравнений выглядит следующим образом. Найти набор чисел 
при подстановке которых вместо переменных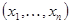 
все уравнения системы 
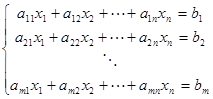обращаются в равенства.
Запишем таблицу чисел, образованную коэффициентами при неизвестных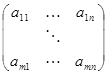 
. В алгебре принято называть прямоугольную таблицу чисел матрицей. Припишем к матрице коэффициентов правые части уравнений 
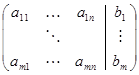отделив их от матрицы коэффициентов вертикальной чертой. Получившаяся матрица называется расширенной матрицей системы линейных уравнений. В дальнейшем нам будет удобнее работать не с системой линейных уравнений, а с её расширенной матрицей.
