Обозначим через M множество решений системы линейных уравнений (элементами множества M являются n-элементные наборы, удовлетворяющие системе линейных уравнений). Преобразование системы линейных уравнений называется равносильным, если оно не меняет её множество решений. Аналогично, преобразование матрицы называется равносильным, если оно соответствует равносильному преобразованию системы линейных уравнений.
Теорема 3.1 Следующие преобразования матрицы являются равносильными:
I. Умножение строки не ненулевое число.
II. Перестановка строк
III. Прибавление к некоторой строке другой строки, умноженной на число.
Доказательство. Равносильность всех трёх преобразований доказывается по одному плану. Приведём этот план. Пусть M – множество решений исходной системы линейных уравнений, а T – множество решений преобразованной системы линейных уравнений (одним из трёх перечисленных преобразований). Взяв элемент x из M, подстановкой убедимся, что он принадлежит T. Тем самым покажем включение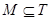 
. Далее, от новой системы линейных уравнений можно вернуться к исходной системе, выполнив обратное преобразование. Значит, по доказанному ранее 
. Объединив оба включения получаем требуемое равенство.
