Производную порядка k от многочлена f(x) обозначим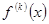 
. При k=0 под 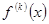будем понимать исходный многочлен.
Лемма 2.1
.
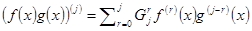Доказательство проведём индукцией по j. При j=1 получаем формулу дифференцирования произведения. Пусть формула верна для j-1. Покажем её справедливость для j. Имеют место равенства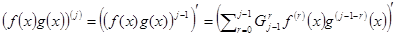 
. Взяв производную от каждого слагаемого, приведя подобные, получим требуемое равенство.
Следствие 2.7 Условие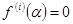 
при i=0,…,k-1 и 
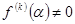равносильно тому, что 
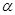- корень f(x) кратности k.
Доказательство. Пусть 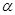- корень f(x) кратности k, тогда 
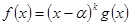, причём 
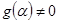. Производная порядка i равна 
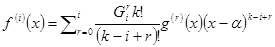. Подставив 
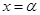получим равенства 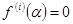при i=0,…,k-1 и 
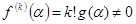. Обратно, разложим f(x) по степеням 
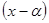, т.е. 
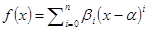. Легко проверить 
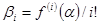и значит 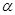- корень f(x) кратности k.
