В ряде случаев необходимо найти многочлен наименьшей степени, у которого на некотором множестве заданы не только его значения, но и значения производных до определенных порядков. Пусть на множестве точек 
заданы значения функции и её производных высших порядков. Под 
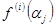будем понимать значение производной порядка i в точке 
. Под производной порядка 0 будем понимать саму функцию. Пусть заданы значения 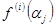, где j=1,…,k и 
.
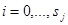Теорема 2.16 (Интерполяционный многочлен Лагранжа - Сильвестра)
Существует единственный многочлен h(x) степени меньше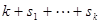 
, удовлетворяющий равенствам 
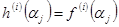, где j=1,…,k и .
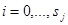Доказательство. Положим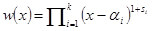 
, 
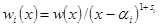. Для i=1,…,k определим числа 
и далее по индукции 
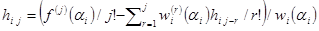, где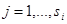 
. Многочлен 
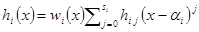удовлетворяет равенствам: 
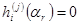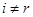при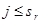 
и 
, и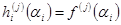 
. Что бы убедится в справедливости равенств найдём производную j порядка 
. Поскольку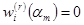 
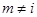при 
и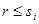 
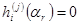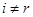, то равенства при и 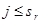установлены. Подставим теперь 
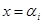и получим 
Подставив вместо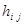 
равное ему выражение, после приведения подобных, получим равенство 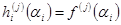. Далее осталось написать интерполяционный многочлен 
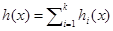. Поскольку степень каждого слагаемого меньше 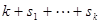, то и степень суммы меньше 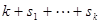. Единственность интерполяционного многочлена покажем методом от противного. Допустим, существует два интерполяционных многочлена h(x) и g(x). Их разность имеет 
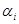корнем кратности не меньше 
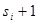и значит, делится на w(x) без остатка. Поскольку степень w(x) заведомо больше чем степень h(x)-g(x), то h(x)=g(x).
